Python:lmfitを使ったカーブフィッティング①

実験データのフィッティングについて頻繁に使う機会があったので自分メモとしてまとめておきます。
フィッティングを行うにあたり、Numpy , Scipyには便利なライブラリがあります。

Numpy :polyfit
Scipy:optimize.leastsq
Scipy:optimize.curve_fit

以上3つが結構有名です。簡単なフィッティングならScipy:optimize.curve_fitを使うのが一番楽だと思います。

Scipy:optimize.curve_fitを使った例

import numpy as np
import scipy.optimize
import matplotlib.pylab as plt

x = np.linspace(0, 2*np.pi, 100)
y1 = np.sin(x)
y2 = 0.5*np.sin(2*x)
y_noise =(y1 + y2)+ 0.08 * np.random.randn(100)

plt.scatter(x,y_noise)

parameter_initial = np.array([0.5, 1.0]) #a, b, c
# function to fit
def func(x, a, b):
    return np.sin(x) +  a*np.sin(b*x)

paramater_optimal, covariance = scipy.optimize.curve_fit(func, x, y_noise, p0=parameter_initial)
print(paramater_optimal)
fitting = func(x,paramater_optimal[0],paramater_optimal[1])

plt.plot(x,fitting,color="red")

このように数行でフィットまでできるので
データがそろっていてモデルがある程度絞れているならこの方法が一番早いです。

ですがちょっと複雑なことしようとするとlmfitに軍配が上がるかもしれません。

lmfitとは？

Non-Linear Least-Squares Minimization and Curve-Fitting for Pythonってサブタイトルがついてる通り非線形最小二乗法を用いたモデルフィットのためのライブラリです。

scipy.optimizeの多くの最適化方法を基にして拡張したものでLevenberg-Marquardt methodの移植からプロジェクトが始まり様々な追加がなされています。
ざっと列挙すると以下があげられる。

Parameter objectsを導入しモデルにアクセスしやすくした
フィッティングアルゴリズムの変更を容易にした
scipy.optimize.leastsqの信頼区間推定の改善
Modelクラスとのカーブフィットが改善（scipy.optimize.curve_fitの機能が拡張）
一般的な線形の多くの組み込みモデルが内包されている。

lmfitを使ってフィッティングを行う

lmfitの導入ですがpipなら簡単にできます。

pip install lmfit

その他Scipy,Numpy,matplotlibなんかが必要だった気がするのでご自分に合った環境づくりをしてください。

サンプルコード

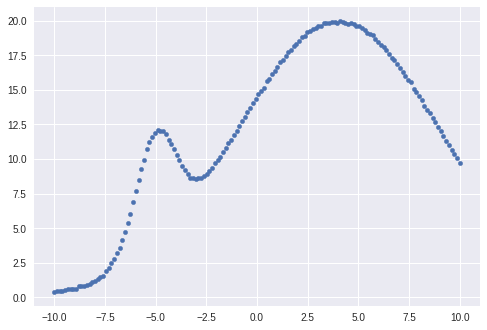
import os
import math
import random

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy import optimize, signal

from lmfit import models

#gaussianを定義(ノイズ入りデータを作るためのダミーモデル）
def gaussian(x, A, μ, σ):
    return A / (σ * math.sqrt(2 * math.pi)) * np.exp(-(x-μ)**2 / (2*σ**2))
  
'''fitするためのノイズ入りデータの作成'''
g_0 = [250.0, 4.0, 5.0]
g_1 = [20.0, -5.0, 1.0]
n = 150
x = np.linspace(-10, 10, n)
# ここでは２つのガウシアンモデルを足し合わせて適当なグラフを作成
y = (gaussian(x, *g_0) + gaussian(x, *g_1)) + 0.05*np.random.randn(n)

fig, ax = plt.subplots()
ax.scatter(x, y, s=20)
'''-----------------------------------------------------------'''

'''lmfitの内蔵モデルの使用'''
model_1 = models.GaussianModel(prefix='m1_')#内包モデルのガウシアンを使用
model_2 = models.GaussianModel(prefix='m2_')#内包モデルのガウシアンを使用
model = model_1 + model_2#コンポジットモデルの作成


'''lmfitの内蔵モデルの初期パラメータセット'''
params_1 = model_1.make_params(center=3.0, sigma=1.0)#ガウシアンのパラメータセット
print(params_1)
params_2 = model_2.make_params(center=-7.0, sigma=1.0)#ガウシアンのパラメータセット
print(params_2)
params = params_1.update(params_2)#update methodにより辞書結合
'''
updateはPythonのビルトインメソッド（もとから入ってる標準関数みたいなもの
param_1とparam_2の辞書をまとめる機能がある
一般的に同名の辞書があるとその中身が上書きされてしまうがprefix='m1_'を付けているため上書きを避けることができる。

'''
output = model.fit(y, params, x=x)
fig, gridspec = output.plot(data_kws={'markersize': 5})

生データ

フィッティング後

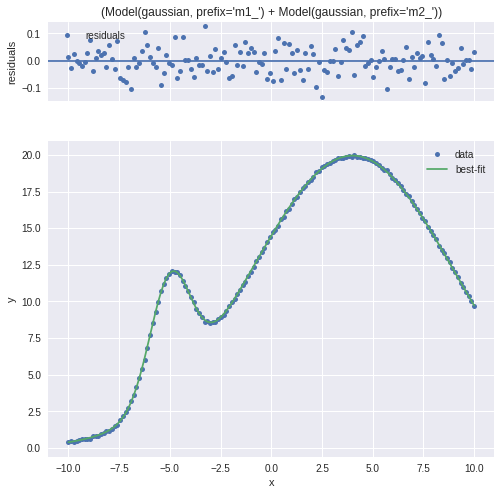
フィッティング後の残差についても出してくれます。
fit後のベストパラメータはoutput.best_valuesに格納されます。

print(output.best_values)

'''-------------------------------------'''
{'m2_sigma': 4.995352955273267, 'm2_center': 4.000094565660837, 'm2_amplitude': 249.88570423583715, 'm1_sigma': 1.0041137260302269, 'm1_center': -4.998780785999739, 'm1_amplitude': 20.079858838765603}