2020/5/6
追記この記事では実データでフィッティングを行っています。
データ自体はご自分で用意していただく形になるのでそのまま実行するだけでは動きません
あくまでlmfitの使い方の一例として捉えていただけると幸いです。
尚初期値、モデルの与え方によっては収束しない、フィッティングがうまく行かないことがあります。(理論を勉強すれば理由はわかるとおもいます。
はじめに
今回は前回の続きでlmfitを使ったフィッティングを試して行きたいと思う。
ほとんどここのパクリだがバグの修正含め解説も入れているので勘弁してほしい
Peak fitting XRD data with Python - Chris Ostrouchov
さっそくやって行こうと思うが
実用的なもので使わないと意味がないので今回はXRD(X-ray Diffraction)のピークフィッティングを例にしてフィッティングしてみたいと思います。
X-ray Diffractionは結晶性物質の解析に用いられる分析で結晶性物質の同定や結晶化度などを求めるときに使います。
以下に例としてゼオライトのXRDピークを示す。

XRDの解析ではこれらのピークをフィットしたりして使うことが多いと思います。
フィッティングにより非晶質ピークと結晶質ピークの面積がわかるのでそれらの割合から結晶化度を求めることが可能です。
全ピークフィットを行うと時間がかかりすぎるので範囲を絞って説明します。
今回は15度~21度範囲でのピークをフィッティングするスキームで進めます。

次にフィットモデルについてだがPeak-like modelsってのがLMFITには内蔵されている
XRDはピーク波形の集まりなのでそれを利用すると楽にフィットできそうである。
その中でもよく使うものを紹介しておく
GaussianModel
LorentzianModel
VoigtModel
where
lmfitのモデル作成
まずはモデルを作る
def generate_model(spec)という関数を定義する
長いのでColabのリンクを貼っておく(リンク先のgenerate_modelって関数)
https://colab.research.google.com/drive/1At5-CseX7jhqPxjSyTk9gbIxC_dFRRU3#scrollTo=EdlAR8AoLbpa&line=26&uniqifier=1
途中でset_param_hintメソッドという新しい項目が出てきます。
これはモデルの最適化を行う際にある程度のヒントを与えるためのメソッドです。
各種説明は以下の通りです。

これ以外はPythonのビルトインメソッドの多様なのでゆっくり読み進めていけば困ることはないと思います。
次にこの関数に与える辞書リストをつくります。
いきなり作るのもあれなので
まずはピーク検出を行うための関数を作る。これにはScipyのfind_peaks_cwtメソッドを利用する。
こちらもColabのリンクで失礼する(update_spec_from_peaks)
https://colab.research.google.com/drive/1At5-CseX7jhqPxjSyTk9gbIxC_dFRRU3#scrollTo=YESpYSpYRyj6&line=2&uniqifier=1
簡単にモデルを与えてあげる
spec = {
'x': theta[int((15-5.0)/0.02):int((21-5.0)/0.02)],
'y': peak[int((15-5.0)/0.02):int((21-5.0)/0.02)],
'model': [
{
'type': 'GaussianModel',
'params': {'center': 26.5, 'height': 10, 'sigma': 1},
},
{
'type': 'GaussianModel',
'params': {'center': 26.14, 'height': 350, 'sigma': 0.1},
},
{
'type': 'GaussianModel',
'params': {'center': 26.8, 'height': 10, 'sigma': 0.08},
},
{
'type': 'GaussianModel',
'params': {'center': 27.12, 'height': 10, 'sigma': 0.1},
},
{
'type': 'GaussianModel',
'params': {'center': 27.5, 'height': 10, 'sigma': 0.1},
},
]
}
次にピーク検出したものをプロット
peaks_found = update_spec_from_peaks(spec, [0,1,2,3,4], peak_widths=(13,)) fig, ax = plt.subplots() ax.scatter(spec['x'], spec['y'], s=4) peaks = np.zeros((len(peaks_found),2)) j = 0 for i in peaks_found: ax.axvline(x=spec['x'][i], c='black', linestyle='dotted') ax.text(spec['x'][i],800, spec['x'][i]) peaks[j,0] = spec['x'][i] peaks[j,1] = spec['y'][i] j = j+1
これを使うとある程度のピーク位置が出てくる
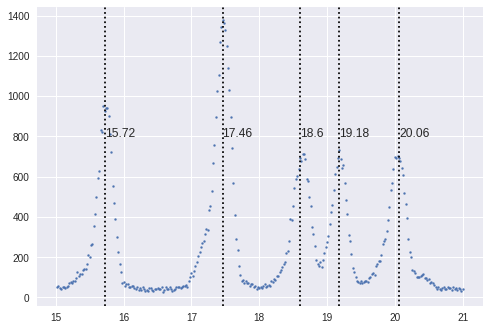
そのままフィッティングしてみる
model, params = generate_model(spec) output = model.fit(spec['y'], params, x=spec['x']) fig, gridspec = output.plot(data_kws={'markersize': 1})

だいたいあっているがフィットしていない部分もある。3,4番目のモデルが当たっていない感があるのでそこのパラメータの与え方を変えてみる
spec['model'][2]['params']['sigma'] = 0.05 spec['model'][3]['params']['sigma'] = 0.05

綺麗にできたみたいなのでピークを分けてみてみる
fig, ax = plt.subplots() ax.scatter(spec['x'], spec['y'], s=4) components = output.eval_components(x=spec['x']) print(len(spec['model'])) for i, model in enumerate(spec['model']): ax.plot(spec['x'], components[f'm{i}_'])

最後にベストパラメータを出して終わり
def print_best_values(spec, output): model_params = { 'GaussianModel': ['amplitude', 'sigma'], 'LorentzianModel': ['amplitude', 'sigma'], 'VoigtModel': ['amplitude', 'sigma', 'gamma'] } best_values = output.best_values print('center model amplitude sigma ') for i, model in enumerate(spec['model']): prefix = f'm{i}_' values = ', '.join(f'{best_values[prefix+param]:8.3f}' for param in model_params[model["type"]]) print(f'[{best_values[prefix+"center"]:3.3f}] {model["type"]:16}: {values}') print_best_values(spec, output) #-------------------------------------------------------------------------------------------- center model amplitude sigma [17.460] GaussianModel : 428.469, 0.129 [20.031] GaussianModel : 253.663, 0.153 [19.180] GaussianModel : 210.520, 0.122 [18.621] GaussianModel : 254.223, 0.148 [15.726] GaussianModel : 284.501, 0.123
まとめ
lmfitを使ったパラメータアシストフィットを行うことができた。
またモデルに推定ヒントを単一値を与えていたが範囲で与えることも可能なためその例も書いておいた。
今回のコード全容は以下にアップロードしているので皆さんのほうでカスタマイズしてみてほしい
https://colab.research.google.com/drive/1At5-CseX7jhqPxjSyTk9gbIxC_dFRRU3
今度はレーベンバーグマルカート法以外のメソッドで得たモデルパラメータを使った複合モデリングについて書いていきたい